ɫ����

In many AI tasks there’s no clear “right” answer. This is especially true for domains like social science, sentiment analysis, and content moderation which remain in high demand. When ground truth is ambiguous, inter-rater reliability (IRR) becomes essential to AI data quality. These metrics help us understand how much of the variation in results is due to evaluator differences versus differences in the data itself.

The key question IRR answers is simple: How much do annotators agree with each other overall?

By measuring how consistently multiple evaluators apply the same criteria, IRR provides an important quality signal. It’s often referred to as inter-annotator agreement, inter-coder reliability, or inter-rater concordance. Without strong agreement, it’s hard to trust downstream insights or the models built on top of that data.

Why IRR Matters in AI Projects

Consider a task where reviewers rate an LLM’s output as “not toxic,” “somewhat toxic,” or “highly toxic.” If one annotator labels a response as “not toxic” and another as “highly toxic,” something is wrong. These inconsistencies could reflect unclear guidelines, poor training, or subjective interpretations – any of which undermine trust in your evaluations.
Reliable labeling is critical to building robust, trustworthy AI systems.

Methods for Measuring Inter-Rater Reliability (IRR)

Several statistical measures exist to evaluate IRR, including:

• Cohen’s kappa
• Fleiss’s kappa
• Krippendorff’s alpha (our focus here)

Krippendorff’s alpha is widely regarded as one of the most robust and flexible IRR measures, refining earlier metrics to assess categorical, ordinal, hierarchical, and continuous data. This versatility gives Krippendorff’s alpha a distinct edge over other IRR measures that may be constrained to certain data types or require complete data sets.

How to Use Krippendorff’s Alpha

A deep knowledge of the algorithm is not necessary to effectively use Krippendorff’s alpha. However, understanding the mathematics at play can provide valuable insights into its application.

Quick Start Guide for Practitioners

Leverage Krippendorff’s alpha with minimal mathematical knowledge by following these five steps:

1. Identify your data type: Nominal, ordinal, interval, or multi-label
2. Calculate alpha
3. Interpret results:
   
   1. α ≥ 0.80 — Reliable
   2. 0.67–0.80 — Tentative
   3. < 0.67 — Unreliable
4. Take action: Use results to refine guidelines, retrain annotators, or improve system design
5. Pair with other metrics: Alpha should be one part of your quality toolkit

Understanding Data Types and Distance Metrics

Krippendorff’s alpha depends on correctly specifying both your data type (e.g. nominal, ordinal, interval) and the distance metric. Using the wrong setting can dramatically skew alpha, either underestimating or overstating agreement.

For example, in a sentiment task with labels like Positive, Neutral, and Negative, treating the labels as nominal assumes all disagreements are equally severe. But if Neutral is conceptually “in the middle,” an ordinal treatment – where Neutral is closer to Positive or Negative than those are to each other – can yield more meaningful scores.

Nominal Data (Single Label)

• Examples: “Dog,” “Cat,” “Bird”; “Positive,” “Negative”
• Binary distance: 0 (match), 1 (no match)
• Used for: Content labels, medical diagnosis, basic sentiment

Nominal Data (Multi-Label)

• Example: Tagging a post as both “Science” and “Art”
• Use: Jaccard distance (ɫ����’s default), Hamming, MASI
• Used for: Multi-topic docs, multi-object image tagging

Ordinal Data

• Ordered labels, uneven intervals (e.g., 1–5 Likert scale)
• Penalises disagreements more as they get further apart
• Used for: Quality ratings, severity levels

Interval Data

• Ordered, equal intervals (e.g., test scores, temperature)
• Use squared difference distance
• Used for: Time-based ratings, continuous assessments

ɫ����’s ADAP platform supports both single-label and multi-label nominal IRR reports. Read our for more.

Real-World Applications of Krippendorff’s Alpha

• Human vs. AI Agreement: Alpha can compare human annotations to AI outputs—useful when validating LLM performance. In the , alpha revealed very low agreement even among native-language fact checkers assessing hate speech. This highlights the challenge of using AI in culturally sensitive domains.
• Sentiment Benchmarking: Datasets like and used Krippendorff’s alpha to assess annotation quality. Interestingly, sentiment tasks showed lower agreement than named entity recognition tasks in the same corpora.
• Medical AI: In clinical settings, α > 0.90 is often required before releasing datasets. on clinical data annotation consistently use Krippendorff's Alpha to ensure annotation reliability meets medical standards before benchmark release.
• Social Media Text Analysis: Krippendorff's alpha can be applied with flexible standards where to remain relevant to the inherent ambiguity in user-generated content.
• Robotics: Krippendorff’s alpga is a valuable metric for datasets like across 63 categories with moderate reliability standards.

These domain-specific applications demonstrate how Krippendorff's Alpha adapts to different risk profiles and annotation complexities, ensuring that benchmark quality standards align with real-world application requirements.

How It Works: The Mathematics Behind Krippendorff’s Alpha

Krippendorff’s Alpha asks: Is the agreement among annotators better than random chance?

Then compares the actual agreement we observe among annotators with what we'd expect if they were making decisions randomly, such that:

• Perfect agreement → α = 1
• Random agreement → α = 0
• Systematic disagreement → α < 0
• The formula for Krippendroff’s alpha is:

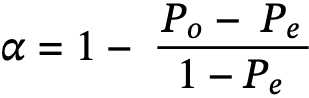
• P_o = Observed Agreement
  This measures the actual agreement observed among the raters. It's calculated using a coincidence matrix that cross-tabulates the data's pairable values.
• P_e = Chance Agreement
  This represents the amount of agreement one might expect to happen by chance. It's an essential part of the formula as it adjusts the agreement score by accounting for the probability of random agreement.
• P_o and P_e = Disagreement
  In the context of Krippendorff's Alpha, disagreement is quantified by calculating both observed and expected disagreements

Let’s walk through a real example.

Example: Annotating for Sentiment Analysis

To illustrate how Krippendorff's Alpha works in practice, let's walk through a sentiment analysis scenario—specifically, an example involving nominal data types. Sentiment categories like Positive, Negative, and Neutral are distinct without any inherent order, making them a classic case of nominal data. Subjective interpretations are common (for instance, deciding whether "okay" is positive or neutral), missing annotations frequently occur in real projects, and the results have a direct impact on LLM training data quality. In such cases, agreement levels among annotators not only demonstrate the utility of the metric but also reveal whether the annotation guidelines are sufficiently clear for consistent decision-making.

Imagine 3 annotators labeling 8 social media posts as Positive, Negative, or Neutral. Here’s what their data annotations look like:

We summarize how often each post received each label, calculate observed and expected agreement, and apply the alpha formula, such that:

• n = 8 (number of posts)
• q = 3 (number of sentiment categories: Positive, Negative, Neutral)
• r = number of times post i received sentiment k
• ��̄ = average number of raters per post

Step 1: Create a table

Count how often each post received each sentiment label:

Step 2: Choose a Distance Metric

For nominal sentiment data, we use binary distance:

• Perfect match = 1 (e.g., Positive vs Positive)
• No match = 0 (e.g., Positive vs Negative)

Step 3: Observed Agreement - P_o

For nominal data, we calculate agreement for each post using the formula:

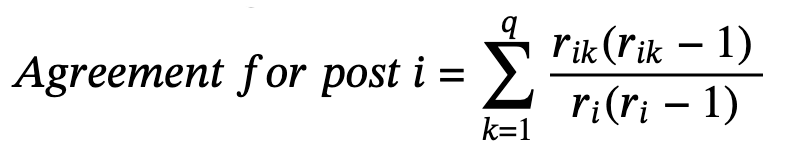
Where:

• r_ik = number of times post i received sentiment k

• r_i = total number of ratings for post i

Let’s work through this part of the example for the first post. We’ll replace r_ik with the value in the table for each post i and rating k, and sum these results. For the first post:

• r_i Positive = 3
• r_i Negative = 0
• r_i Neutral = 0
• r_i = 3 (total ratings for post)

Calculation for Post 1 Agreement

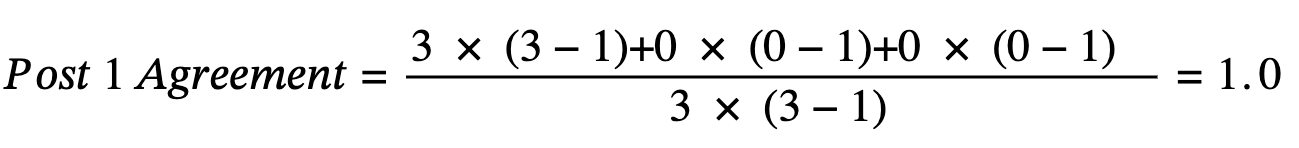
This makes intuitive sense: when all annotators agree perfectly (all chose "Positive"), the agreement is 1.0 (perfect agreement)

We do this for every post in the table and sum the results

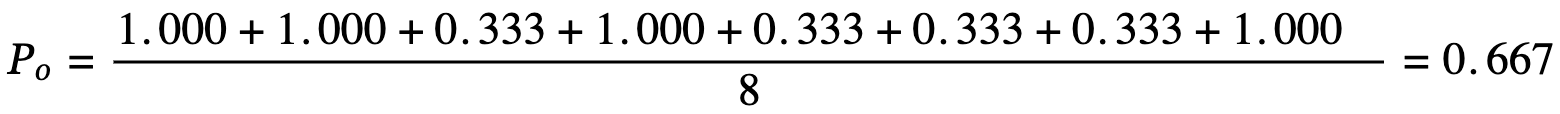
In this example, the observed agreement P_o turns out to be 0.667.

Step 3: Expected Agreement (P_e)

Now we calculate what agreement we'd expect by chance, based on the overall frequency of each sentiment label.

Count total label occurrences across all posts:

Calculate probabilities for each sentiment:

• π_positive = 8/23 = 0.348
• π_negative = 8/23 = 0.348
• π_neutral = 7/23 = 0.304

Calculate expected agreement (sum of squared probabilities):

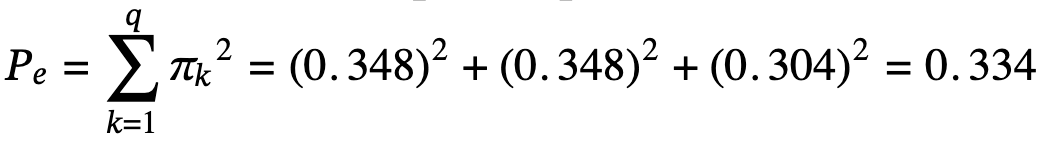
Step 4: Final Calculation

Now plug both values into the formula:

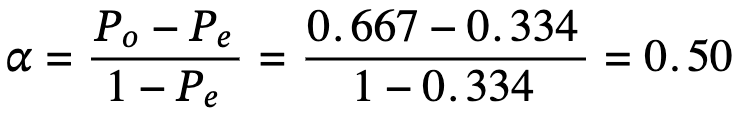
Interpreting the Results

Krippendorff's Alpha values range from -1 to +1, where:

• >0.8—This range is reliable. If you apply Krippendorff’s alpha to your data, and you get a result of 0.8 or higher, you have high agreement and a dataset that you can use to train your model.
• 0.67–0.8—This range has low reliability. It is likely that some of the labels are highly consistent and others are not.
• 0–0.67—At less than 0.67, your dataset is considered to have low reliability. Something is probably wrong with your task design or with the annotators.
• 0—Random distribution.
• -1—Perfect disagreement.

An alpha of 0.50 is considered low reliability. It likely indicates the need for better training, clearer guidelines, or a refinement of the labeling schema.

Common Pitfalls and Fixes

Beyond Agreement: Building Better Annotation Pipelines

Even strong agreements don’t guarantee high-quality data. Annotators can unanimously miss subtle but important features.

Krippendorff’s Alpha should be used alongside:

• Ground truth comparisons
• Regular audits
• Contributor training
• Confidence scores
• Task decomposition
• Metrics like accuracy, precision, and recall

Relying solely on agreement risks reinforcing shared bias. By combining alpha with broader human-in-the-loop techniques, teams can better diagnose reliability issues and produce stronger datasets.

Final Takeaway

Krippendorff’s Alpha is a powerful, flexible tool for measuring annotation consistency—but it’s not the whole story. To build trustworthy, high-performing AI systems, teams need a multi-layered approach to data quality.

Want to learn more about quality metrics?
Check out ɫ����’s guide to AI data quality or get in touch to explore how we help teams improve data reliability at scale.

‍